Question

Heat is escaping at a constant rate, (dQ/dt is constant) through the walls of a long cylindrical pipe. Find the temperatureT at a distance r from the axis of the cylinder if the inside wall has radius r=1, and temperatureT=100, and the outside wall has r=2, andT=0.

Answer 1

`T = (-1)/(6.93*10^(-3))ln(r)+100`

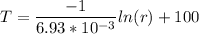
Explanation:

Hello,

To solve this, we can use the famous Fourier's Law of Heat Conduction

`(dQ)/(dt) = -kA(dT)/(dr)`

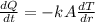
What do we know so far?

• Cylinder with radii
  `r_1 = 1 & r_2 = 2`
• Surface of Area of Cylinder is
  `A = 2\pi rl`
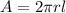
• Inner temperature :
  `T_1 = 100`

• Outer temperature:
  `T_2 = 0`
• Heat dissipation rate is constant:
  `(dQ)/(dt) = Q`

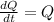
When solving keep in mind that the values provided are "boundary conditions" that we'll need when solving this differential equation.

`(dQ)/(dt) = -kA(dT)/(dr)\\\\Q = -k(2\pi rl)(dT)/(dr)\\(1)/(r)dr = (-2k\pi l )/(Q) dt`

`\int\limits^(r_1)_(r_2) {(1)/(r)} \, dr = \int\limits^(T_2)_(T_1) {(-2k\pi l )/(Q)} \, dT`

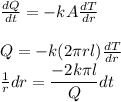
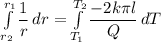
keep in mind that the whole term
`(2k\pi l )/(Q)` is a constant and will not take part in the integration, so we can just call this whole term
`C`

`\int\limits^(r_2)_(r_1) {(1)/(r)} \, dr = {(-2k\pi l )/(Q)} \int\limits^(T_2)_(T_1) \, dT \\\int\limits^(r_2)_(r_1) {(1)/(r)} \, dr = -C \int\limits^(T_2)_(T_1) \, dT`

`ln(r_2) -ln(r_1) = -C(T_2 - T_1)`

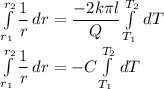
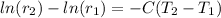
We can simplify now,

`ln((r_2)/(r_1)) = -C(T_2 - T_1)`

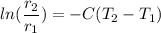
This is our solution to the differential equation, lets call it Eq(1)

Putting all the known values, and forming an equation we can find the value of C

`ln((r_2)/(r_1)) = -C(T_2 - T_1)\\ln((2)/(1)) = -C(0-100)\\C = (ln(2))/(100) \\C = 6.931 * 10^(-3) = 0.00693`

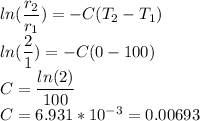
We can put this in value in our original equation Eq(1)

`ln((r_2)/(r_1)) = -C(T_2 - T_1)\\T_2 = (1)/(-C)ln((r_2)/(r_1))+T_1\\T_2 = (-1)/(6.93*10^(-3))ln((r_2)/(r_1))+T_1\\`

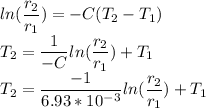
This is our general equation, but the question is asking to find the temperature
`T` at a distance r, i.e
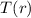`T(r)`, given that
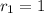`r_1 = 1` and
`T_1 = 100`, this means that the above equation needs to be converted in the form such that
`T` is only a function of
`r`

`T_2 = (-1)/(6.93*10^(-3))ln((r_2)/(r_1))+T_1\\T_2 = (-1)/(6.93*10^(-3))ln((r_2)/(1))+100\\`

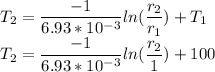
We can remove the subscripts if we like

`T = -(1)/(6.93*10^(-3))ln(r)+100`

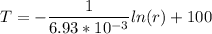
Finally, this is our equation for the outer temperature of the cylinder at any distance r