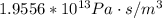Question

An arteriole has a radius of 25 m and it is 1000 m long. The viscosity of blood is 3 x 10-3 Pa s and its density is 1.055 g cm-3. Assume the arteriole is a right circular cylinder. A. Assuming laminar flow, what is the resistance of this arteriole?

Answer 1

To solve this problem it is necessary to apply the concepts related to the Hagen-Poiseuille equation law, which is a physical equation for the description of nonideal fluid dynamics, that is the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross-section. The expression can be extrapolated to the calculation of resistance through an analogy of Ohm's law. Mathematically the equation that describes this phenomenon can be described as,

`R = (8\mu L)/(\pi R^4)`

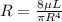
Where,

R = Resistance

L = Length of pipe

`\mu =` Dynamic viscosity

R = Pipe radius

Our values are given as,

`\mu = 3*10^(-3)Pa\cdot s`

`L = 1000*10^(-6)m`

`R = 25*10^(-6)m^4`

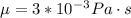
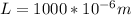
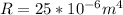
Replacing at the previous equation we have,

`R = (8(3*10^(-3))(1000*10^(-6)))/(\pi (25*10^(-6))^4)`

`R = 1.9556*10^(13)Pa\cdot s/m^3`

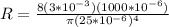
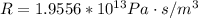
Therefore the resistance of this arteriole is
`1.9556*10^(13)Pa\cdot s/m^3`