Answer:
The graph is attached below.
Same asymptote as similarity and the slopes are different.
Explanation:
We need to find the graph of

When
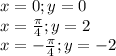
and
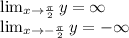
The asymptotes are
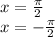
If we compare the graphs of
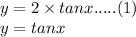 ......(2)
......(2)
then the similarities are, they have same asymptote.
Difference between them is the rate of change that is the slope of the equations.