Answer:
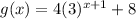
Explanation:
Given:
The original function is given as:
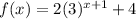
The above function is stretched vertically by a factor of 2 to form the graph of
 .
.
According to the rule of function transformations, when the graph of a function is stretched in the vertical direction by a factor of 'C', where, 'C' is a number greater than 1, then the function rule is given as:
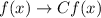
Therefore, the function is multiplied by a factor of 'C' to get the equation of the stretched function.
Here, the the value of 'C' is 2. So, the equation of
 is given as:
is given as:
![g(x)=2f(x)\\g(x)=2[2(3)^(x+1)+4]\\g(x)=4(3)^(x+1)+8](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4dl2v1r8mg7un0ow4vtshpfayq0b5qj173.png)
Therefore, the equation of
 is
is
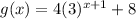 .
.