Question

A coffee merchant has two types of coffee beans, one selling for $9 per pound and the other for $15 per pound. The beans are to be mixed to provide 100 lb of a mixture selling for $13.50 per pound. How much of each type of coffee bean should be used to form 100 lb of the mixture?

Answer 1

To form 100 lb of the mixture we need 25 lbs of $9 coffee beans and 75 lbs of $15 coffee beans.

Explanation:

Let x be the number of pounds of $9 coffee beans and y be the number of pounds of $15 coffee beans.

We know that the mixture must weigh 100 lb

`x+y=100`

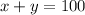
and the total cost per pound is given by

`9x+15y=13.50\cdot 100\\9x+15y=1350`

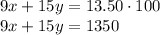
Now, we can solve the system of equations

`\begin{bmatrix}x+y=100\\ 9x+15y=1350\end{bmatrix}`

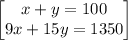
Isolate x for
`x+y=100`

`x=100-y`

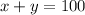
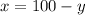
Substitute
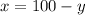`x=100-y` into the second equation

`9\left(100-y\right)+15y=1350`

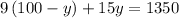
Isolate y

`900-9y+15y=1350\\900+6y=1350\\900+6y-900=1350-900\\6y=450\\(6y)/(6)=(450)/(6)\\y=75`

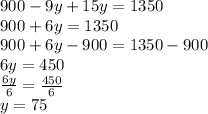
For
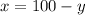`x=100-y` substitute y = 75

`x=100-75\\x=25`

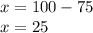
To form 100 lb of the mixture we need 25 lbs of $9 coffee beans and 75 lbs of $15 coffee beans.