Question

A company that offers tubing trips down a river rents tubes for a person to use for $20 and "cooler" tubes to carry food and water for $12.50. A group spends $270 to rent a total of 15 tubes. How many of each type of tube does the group rent?

Answer 1

The number of river rent tubes are 11 and the number of cooler tubes are 4.

Explanation:

Given,

Total number of tubes = 15

Total amount of money spent = $270

Price of river rent tube = $20

Price of cooler tube = $12.50

Solution,

Let the number of river rent tube be x.

And the number of cooler tube be y.

So,

Total number of tubes = The number of river rent tube + The number of cooler tube

On substituting the values, we get;

`x+y=15\ \ \ \ \ \ equation\ 1`

Now,

Total amount of money spent = Price of river rent tube X The number of river rent tube + Price of cooler tube X The number of cooler tube

So,

`20x+12.50y=270\ \ \ \ \ \ equation\ 2`

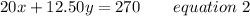
Now multiplying equation 1 by 20 and then subtract equation 2 from it, we get;

`20(x+y)=20*15\\20x+20y=300`

`(20x+20y=300) - (20x+12.50y=270)\\\\7.50y=30\\\\y=(30)/(7.50) =(300)/(75) =4`

`y=4`

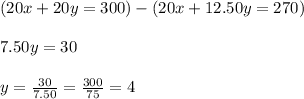
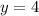
On substituting the value of y in equation 1, we get the value of x;

`x+y=15\\x+4=15\\x=15-4=11`

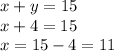
Thus the number of river rent tubes are 11 and the number of cooler tubes are 4.