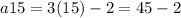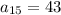Answer:
a)
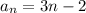
b)
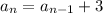
c)
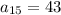
Explanation:
Arithmetic Sequences
In an arithmetic sequence, each number is obtained as the previous number plus or minus a constant value known as the common difference. The general term for an arithmetic sequence is
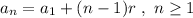
where a_1 is the first term, r the common difference and n the number of terms
If we wanted to express the sequence in the recursive form, we only need to write each term as a function of the previous term.
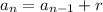
a) We can see in the graph the following sequence: 1, 4, 7 where clearly each term equals the previous term plus 3 (the common difference). So our general term is
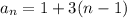
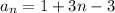
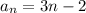
b) The recursive expression is
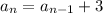
c) To determine
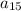 , we use n=15 in the general term
, we use n=15 in the general term