Answer:
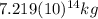
Step-by-step explanation:
According to the Law of Universal Gravitation:
The force
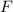 exerted between two bodies of masses
exerted between two bodies of masses
 and
and
 and separated by a distance
and separated by a distance
 is equal to the product of their masses and inversely proportional to the square of the distance.
is equal to the product of their masses and inversely proportional to the square of the distance.
Written in a mathematicall form is:
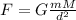 (1)
(1)
Where:
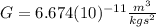 is the gravitational constant
is the gravitational constant
 is the mass of the object
is the mass of the object
 is the mass of the planet
is the mass of the planet
 is the distance from the center of the planet and the object
is the distance from the center of the planet and the object
In addition, this gravitational force is also equal to:
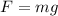 (2)
(2)
Where
 is the acceleration due gravity in this planet
is the acceleration due gravity in this planet
On the other hand, we are told the astronaut walks straight ahead, and find itself returning to its spacecraft from the opposite side after completing a lap of
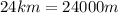 . This means the measure of the circumference
. This means the measure of the circumference
 of this planet is:
of this planet is:
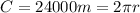 (3)
(3)
Where
 is the radius of the planet.
is the radius of the planet.
Finding
 :
:
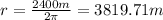 (4)
(4)
At this point we know the distance between the center of the planet and its surface. If we want to know the distance between the center and any of the mentioned objects we will have to add its height
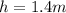 :
:
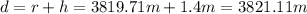 (5)
(5)
Now, we need to find the acceleration due gravity in this planet, which can be found by the following equation of an object falling to ground from rest:
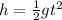 (6)
(6)
Where
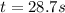
Isolating
 :
:
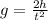 (7)
(7)
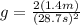 (8)
(8)
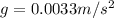 (9)
(9)
Now that we have all the data, we can find the mass by making (1)=(2):
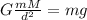 (10)
(10)
Isolating
 :
:
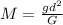 (11)
(11)
 (12)
(12)
Finally:
 This is the mass of the planet
This is the mass of the planet