Answer:
Since our calculated value is lower than our critical value,
 , we have enough evidence to reject the null hypothesis at 5% of significance. So we have a significant difference between th interest rates paid by the two states.
, we have enough evidence to reject the null hypothesis at 5% of significance. So we have a significant difference between th interest rates paid by the two states.
Explanation:
1) Data given and notation
 represent the mean for Georgia
represent the mean for Georgia
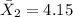 represent the mean for Ohio
represent the mean for Ohio
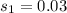 represent the population standard deviation for Georgia
represent the population standard deviation for Georgia
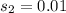 represent the population standard deviation for Ohio
represent the population standard deviation for Ohio
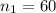 sample size for the group Georgia
sample size for the group Georgia
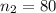 sample size for the group Ohio
sample size for the group Ohio
z would represent the statistic (variable of interest)
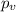 represent the p value
represent the p value
2) Concepts and formulas to use
We need to conduct a hypothesis in order to check if the mean's are different, the system of hypothesis would be:
H0:
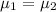
H1:
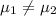
If we analyze the size for the samples both are higher than 30, so for this case is better apply a z test to compare means, and the statistic is given by:
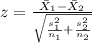 (1)
(1)
z-test: Is used to compare group means. Is one of the most common tests and is used to determine whether the means of two groups are equal to each other.
3) Calculate the statistic
We have all in order to replace in formula (1) like this:
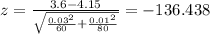
4) Find the critical value
In order to find the critical value we need to take in count that we are conducting a two tailed test, so we are looking for thwo values on the normal standard distribution that accumulates 0.025 of the area on each tail. We can us excel or a table to find it, for example the code in Excel is:
"=NORM.INV(1-0.025,0,1)", and we got
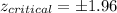
5) Statistical decision
Since our calculated value is lower than our critical value,
 , we have enough evidence to reject the null hypothesis at 5% of significance. So we have a significant difference between th interest rates paid by the two states.
, we have enough evidence to reject the null hypothesis at 5% of significance. So we have a significant difference between th interest rates paid by the two states.