Question

If the correlation between height and weight of a large group of people is 0.74, find the coefficient of determination (as a percent) and explain what it means. Assume that height is the predictor and weight is the response, and assume that the association between height and weight is linear.

A. The coefficient of determination is 54.76%. Therefore, 54.76% of the variation in height can be explained by the regression line.
B. The coefficient of determination is 54.76%. Therefore, 54.76% of the variation in weight can be explained by the regression line.
C. The coefficient of determination is 74%. Therefore, 74% of the variation in height can be explained by the regression line.
D. The coefficient of determination is 74%. Therefore, 74% of the variation in weight can be explained by the regression line.

Answer 1

B. The coefficient of determination is 54.76%. Therefore, 54.76% of the variation in weight can be explained by the regression line.

Explanation:

The correlation coefficient is a "statistical measure that calculates the strength of the relationship between the relative movements of two variables". It's denoted by r and its always between -1 and 1.

The coefficient of determination is a measure to quantify how a model explains an dependent variable.

The formula for the correlation coeffcient is given by:

`r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))`

The formula for the coefficient of determination is
`r^2`

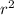
In our case the correlation coefficient obtained was 0.74

And the determination coefficient is
`R=0.74^2 =0.5476`, and if we convert this into % we got 54.76%

Assume that height is the predictor (X) and weight is the response (Y)

And the best answer for this case is:

B. The coefficient of determination is 54.76%. Therefore, 54.76% of the variation in weight can be explained by the regression line.