Question

Sketch the following to help answer the question. Kite QRST has a short diagonal of QS and a long diagonal of RT. The diagonals intersect at point P. Side QR = 10m and diagonal QS = 12m. Find the length of segment RP.

A. 6m
B. 8m
C.10m
D.12m

Answer 1

B. 8m

Explanation:

Given:

The figure is a kite having points QRST.

It has short diagonal QS.

Long diagonal RT

Diagonal Intersect at point P.

side QR = 10m

Diagonal QS = 12m

We need to find the length of segment RP.

According Diagonal Property of kite.

It states that Diagonals of Kite perpendicularly bisects each other.

QP = PS

RP = PT

But QS = QP + PS

QS = QP + QP

QS = 2 QP

QP =
`(1)/(2)` QS =
`(1)/(2)* 12 = 6 m`

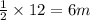
Now In Δ QPR

m∠ P = 90° (Diagonals of a kite is perpendicular to each other)

Now by Pythagoras theorem;

`QR^2 = QP^2+RP^2\\RP^2 = QR^2 - QP^2\\RP^2 = (10)^2- (6)^2\\RP^2 = 100 -36\\RP^2=64\\RP = √(64) =8\ m`

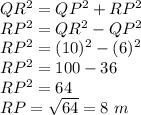
Hence the Length of segment RP is 8m.