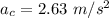Question

if you run around a circle at 4.5 m/s and the circle has a radius of 7.7 m, what is your centripetal acceleration?

Answer 1

Centripetal acceleration,

`a_(c) =2.63\ m/s^(2) }`

Step-by-step explanation:

Centripetal acceleration:

Centripetal acceleration is the idea that any object moving in a circle, in something called circular motion, will have an acceleration vector pointed towards the center of that circle.

Centripetal means towards the center.

Examples of centripetal acceleration (acceleration pointing towards the center of rotation) include such situations as cars moving on the cicular part of the road.

An acceleration is a change in velocity.

Formula for Centripetal acceleration:

`a_(c) =((velocity)^(2) )/(radius)`

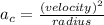
Given here,

Velocity = 4.5 m/s

radius = 7.7 m

To Find :

`a_(c) = ?`

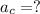
Solution:

We have,

`a_(c) =((velocity)^(2) )/(radius)`

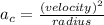
Substituting given value in it we get

`a_(c) =((4.5)^(2))/(7.7) \\\\a_(c) =(20.25)/(7.7)\\\\a_(c) =2.629\ m/s^(2) \\\\\therefore a_(c) =2.63\ m/s^{2`

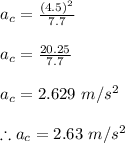
Centripetal acceleration,

`a_(c) =2.63\ m/s^(2) }`