Answer:
3.
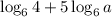
Explanation:
Given:
The logarithm to expand is given as:
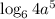
We use the following property of logarithm to expand it into sum of 2 logarithms:
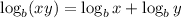
Therefore,
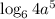 =
=
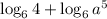
Now, we further simplify the second logarithm using the following property:
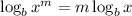
Therefore,
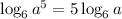
This gives,
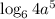 =
=
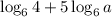
Therefore, the correct choice is choice 3.