Answer:

Step-by-step explanation:
The gravitational potential energy
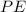 is the energy that a body or object possesses, due to its position in a gravitational field. That is why this energy depends on the relative height of an object with respect to some point of reference and associated with the gravitational force.
is the energy that a body or object possesses, due to its position in a gravitational field. That is why this energy depends on the relative height of an object with respect to some point of reference and associated with the gravitational force.
In the case of the Earth, in which the gravitational field is considered constant, the value of the gravitational potential energy is given by:
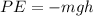 (1)
(1)
Where:
 ia the mass of water
ia the mass of water
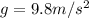 is the acceleration due gravity
is the acceleration due gravity
 is the height of the object
is the height of the object
Now, if we want to calculate the change in gravitational potential energy
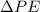 we have to use the following equation:
we have to use the following equation:
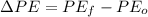 (2)
(2)
Being
 the initial potential energy where
the initial potential energy where
 is the initial height and
is the initial height and
 the final potential energy where
the final potential energy where
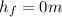 is the final height in the waterfall.
is the final height in the waterfall.
Solving:
 (3)
(3)
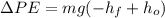 (4)
(4)
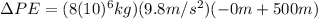 (5)
(5)
Finally:
 (6)
(6)