Question

The explicit rule for an arithmetic sequence is a, -87+(-1.4)(n-1) What is the value of the 47th term? Round to them

tenth, if necessary
557
45.6
65.8

Answer 1

There is typo error in the question. Here is the corrected question:

The explicit rule for an arithmetic sequence is
`a_n=8.7+(-1.4)(n-1)`. What is the value of the 47th term? Round to the nearest tenth, if necessary.

A. –55.7

B. –26.4

C. 45.6

D. 65.8

Answer:

-55.7

Explanation:

Given:

The explicit rule for the given arithmetic sequence is:

`a_n=8.7+(1.4)(n-1)`

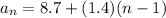
Now, the 47th term is nothing but the value of 'n' as 47.

Plug in the value of 'n' as 47 in the above rule and determine the 47th term represented by
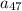`a_(47)`. This gives,

`a_(47)=8.7-1.4(47-1)\\a_(47)=8.7-1.4(46)\\a_(47)=8.7-64.4\\a_(47)=-55.7`

Therefore, the 47th term of the given arithmetic sequence is -55.7. So, the first option is correct.