2 Answers

Edeph · Answer 1 · 2020-10-16T21:03:59+0000

Answer:

The magnitude of the force of gravity on that person is 784 Newton.

Step-by-step explanation:

The weight is a force acting on an object as a consequence of gravity and is defined as:

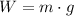$W = m \cdot g$ (1)

Where m is the mass and g is the value of the gravity.

Finally, making the assumption that the person is in the Earth and using equation 1 it is gotten:

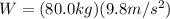
W = (80.0 kg)(9.8m/s^(2))

Remember that the value of g change in function of the radius and mass of the planet ({tex]g = \frac{G\cdotM}{R^{2}}[/tex])

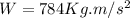
W = 784 Kg.m/s^(2)

But
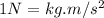
1 N = kg.m/s^(2)

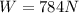
W = 784 N

Therefore, the magnitude of the force of gravity on that person is 784 Netwon.

Please log in or register to add a comment.