Answer:
First number = 3
Second number = 7
Explanation:
Let one number be =

Let other number be =

"One number added to three times another number is 24" can be written mathematically as:
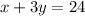
Five times the first number added to three times the other number is 36 can be written mathematically as:
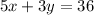
So, we have a system of equation as:
A)
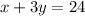
B)
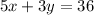
Solving for
 and
and
 using elimination.
using elimination.
Multiplying equation A with -1 and adding it to B to eliminate

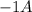 would be
would be
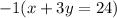

 would be
would be

+
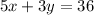
We have,
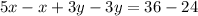
Thus
 is eliminated. Now, we can solve for
is eliminated. Now, we can solve for

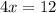
Dividing both sides by 4.
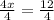
∴

Plugging in
 in equation A to solve for
in equation A to solve for

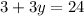
Subtracting both sides by 3.
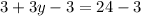
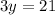
Dividing both sides by 3.

∴
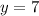
So, first number = 3
Second number = 7