Question

Let ????C be the positively oriented square with vertices (0,0)(0,0), (2,0)(2,0), (2,2)(2,2), (0,2)(0,2). Use Green's Theorem to evaluate the line integral ∫????10y2x????x+4x2y????y∫C10y2xdx+4x2ydy.

Answer 1

-48

Explanation:

Lets call L(x,y) = 10y²x, M(x,y) = 4x²y. Green's Theorem stays that the line integral over C can be calculed by computing the double integral over the inner square of Mx - Ly. In other words

`\int\limits_C {L(x,y)} \, dx + M(x,y) \, dy =  \int\limits_0^2\int\limits_0^2 (M_x - L_y ) \, dx \, dy`

Where Mx and Ly are the partial derivates of M and L with respect to the x variable and the y variable respectively. In other words, Mx is obtained from M by derivating over the variable x treating y as constant, and Ly is obtaining derivating L over y by treateing x as constant. Hence,

• M(x,y) = 4x²y
• Mx(x,y) = 8xy
• L(x,y) = 10y²x
• Ly(x,y) = 20xy
• Mx - Ly = -12xy

Therefore, the line integral can be computed as follows

`\int\limits_C {10y^2x} \, dx + {4x^2y} \,dy = \int\limits_0^2\int\limits_0^2 -12xy \, dx \, dy`

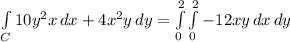
Using the linearity of the integral and Barrow's Theorem we have

`\int\limits_0^2\int\limits_0^2 -12xy \, dx \, dy = -12 \int\limits_0^2\int\limits_0^2 xy \, dx \, dy = -12 \int\limits_0^2(x^2y)/(2) |_(x = 0)^(x=2) \, dy = -12 \int\limits_0^22y \, dy \\= -24 ( (y^2)/(2) |_0^2) = -24*2 = -48`

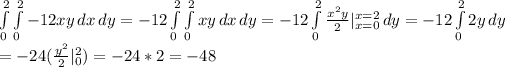
As a result, the value of the double integral is -48-