Question

A nylon guitar string is fixed between two lab posts 2.25 m apart. The string has a linear mass density of μ = 6.60 g/m and is placed under a tension of 170.00 N. The string is placed next to a tube, open at both ends, of length L. The string is plucked and the tube resonates at the n = 3 mode. The speed of sound is 343 m/s. What is the length of the tube?

Answer 1

14.4259 m

Step-by-step explanation:

F = Force on string = 170 N

`\mu` = Linear density = 6.6 g/m

L = Length of string = 2.25 m

n = Mode = 3

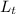`L_t` = Length of tube

v = Speed of sound in air = 343 m/s

Speed of wave is given by

`u=\sqrt{(F)/(\mu)}\\\Rightarrow u=\sqrt{(170)/(6.6* 10^(-3))}\\\Rightarrow u=160.492\ m/s`

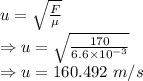
Frequency of wave of the string is given by

`f_s=(u)/(2L)\\\Rightarrow f_s=(160.492)/(2* 2.25)\\\Rightarrow f_s=35.665\ Hz`

Frequency of wave of the tube is given by

`f_t=(nv)/(2L_t)\\\Rightarrow L_t=(nv)/(2f_t)\\\Rightarrow L_t=(3* 343)/(2* 35.665)\\\Rightarrow L_t=14.4259\ m`

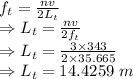
The length of the tube is 14.4259 m