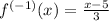Whats the inverse of y=3x+5

Question

asked Jul 19, 2020 110k views

1 Answer

Mandar Belkunde · Answer 1 · 2020-07-26T14:46:02+0000

Answer:

The inverse of y is

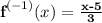
$\textbf{f}^(( -1 ))( x ) = \frac{\textbf{x-5}}{\textbf{3}}$

Explanation:

To Find the inverse of
y = 3x+5

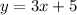
STEP 1: Stick a "y" in for the "f(x)"

y = 3x+5

STEP 2: Switch the x and y ( because every (x, y) has a (y, x) partner! ):

x = 3y+5

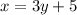
STEP 3: Solve for y:

{x-5}=3y

y=(x-5)/(3)

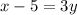
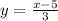
STEP 4: Stick in the inverse notation,
f^(( -1 ))( x )

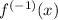
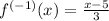
f^(( -1 ))( x ) =(x-5)/(3)

Therefore the inverse of y is

f^(( -1 ))( x ) = (x-5)/(3)