Question

Of a random sample of 381 high-quality investment equity options, 191 had less than 30% debt. Of an independent sample of 166 high-risk investment equity options, 145 had less than 30% debt. Test, against a two sided alternative, the null hypothesis that the two population proportions are equal.

Answer 1

As we have calculated Z = -8.2345 THEREFORE critical value is -1.96 hence there is significant difference , neglect null hypothesis.

and two population are not equal

Explanation:

Given data:

Assuming null hypothesis be Hypothesis O (P1 = P2)

Assuming alternate hypothesis be Hypothesis A (P1 is not equal to P2)

`n_1 = 381`

`p_1 =(191)/(381) = 0.5013`

`n_2 =166`

`p_2 = (145)/(166) = 0.8735`

`P = (n_1 p_1 + n_2 p_2 )/(n_1 + n_2)`

`P = (191 + 145)/(381+166) = 0.6143`

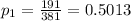
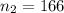
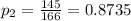
Q = 1 - P = 0.3857

`SE =\sqrt{PQ ((1)/(n_1) + (1)/(n_2))}`

`= \sqrt{0.6143 * 0.3857 * ((1)/(381) + (1)/(166))}`

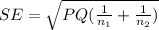
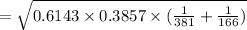
SE = 0.0452

test statics

`Z = ((p_1 - p_2))/(SE)`

`Z = (0.5013 - 0.8735)/(0.0452) = -8.2345`

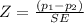
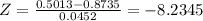
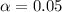`\alpha = 0.05` [taken 5% significance level]

from standard z table , critical value of
`Z = \pm 1.96`

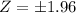
As we have calculated Z = -8.2345 THERFORE critical value is -1.96 hence there is significant difference , neglect null hypothesis.

and two population are not equal