Question

Write the standard form of the equation of the line with slope -1 and y-intercept 1

Answer 1

`x + y = 1`.

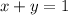Explanation:

In general,
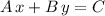`A \,x + B\, y = C` is the standard form of a line. Note that
`A`,
`B`, and
`C` are constants that can be equal to zero.

The question provided the slope and the y-intercept of the line in question. Hence, start with the slope-intercept form and rewrite to produce the standard form.

The slope-intercept form of a line is in the form

`y = m \, x + b`,

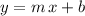where

• 
  `m` is the slope of the line, and
• 
  `b` is the y-intercept of the line (not the x-intercept.)

In this case,

• 
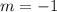  `m = -1`, and
• 
  `b = 1`.

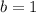Hence the line in the slope-intercept form:

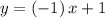`y = (-1) \, x +1`, or, simply,
`y = -x + 1`.

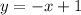Rearrange the equation to produce the standard form. Add
`x` to both sides of the equation:

`x + y = x - x + 1`.

`x + y = 1`.

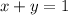And that's the standard form of this line. In this case,
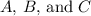`\text{$A$, $B$, and $C$}` are all equal to
`1`.