Question

A rectangular field is 100 meters wide and 140meters long. Give the length and width of another rectangular field that has the same perimeter but a smaller area.

Answer 1

The length of rectangle 2 = 80 m

The width of rectangle 2 = 160 m

Explanation:

The width of rectangle 1 = 100 m

The length of rectangle 1 = 140 m

Now the PERIMETER OF A RECTANGLE = 2 (L+B)

So, here the Perimeter of R 1 = 2 ( 100 + 140) = 2 x 240 = 480 m

Also, AREA OF THE RECTANGLE = LENGTH x WIDTH

So, here the Area of R 1 = 100 x 140 = 14,000 sq m

Now, in the Rectangle 2:

Let us assume the width of rectangle 2 = x

Assume the length of rectangle 2 = y

Now,Perimeter of rectangle 2= Perimeter of rectangle 1

⇒ 2 (x + y) = 480 m ......... (1)

Also, Area of rectangle 2 < Area of rectangle 1

⇒ x y < 14,000 ..... (2)

Now, solving both the equations, we get

(x +y ) = 240 ⇒ y = 240 - x

x y < 14,000

Substituting y = 240 - x in (2), we get:

x (240-x) < 14,000

or,
`0< x^2 -240x +14,000`

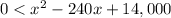
Solving the above equation, we get

x < 140

Now, if we take x = 80, then y = 160

So, for x = 80, y = 160,

Perimeter = 2 ( 80 + 160) = 240 m

Area = x y = 80 x 160 = 12,800 < 14,000

Hence, one possible pair of solution for (x,y) =(80,160)