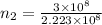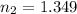Answer:
a)
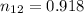
b)
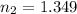
c)
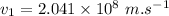
d)
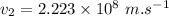
Step-by-step explanation:
Given:
- refractive index of liquid medium 1 (with respect to air),
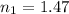
- angle of incidence in medium 1,
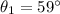
- angle of refraction in medium 2,

(a)
According to Snell's Law:
refractive index of medium 2 with respect to medium 1:
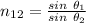
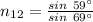
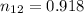
(c)
Now the other form of Snell's law:
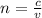 ..............................(2)
..............................(2)
where:
c = speed of light in air
n = refractive index of the medium with respect to air
v = speed of light in medium
Using eq. (2) for medium 1:
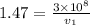
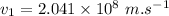
(d)
Using eq. (2) for medium 2:
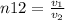
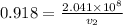
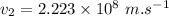
(b)
Now, refractive index of the medium 2 with respect to air