Answer:
A) {-13,-5}
Explanation:
Given expression:
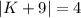
We need to solve for
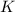
Since
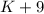 lies in the absolute brackets, so we can write the solution as (
lies in the absolute brackets, so we can write the solution as (
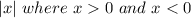 ) :
) :
For
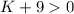
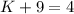
For
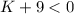
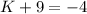
Solving for K individually.
Subtracting both sides by 9.
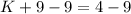 and
and
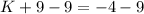
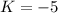 and
and
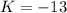
So, the solution can be written as {-13,-5}