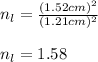Question

When a liquid is introduced into the air space between the lens and the plate in a Newton's-rings apparatus, the diameter of the tenth ring changes from 1.52 cm to 1.21 cm. Find the index of refraction of the liquid.

Answer 1

`n_l=1.58`

Step-by-step explanation:

Newton's ring equation relates the initial and final diameter of the ring, to the index of refraction of the air and the index of refraction of the liquid between the lens and the plates, as follows:

`n_ld_f^2=n_ad_i^2`

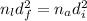
Solving for :

`n_l=n_a(d_i^2)/(d_f^2)\\`

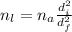
Recall that the refractive index of the air is 1. So, replacing the given diameters:

`n_l=((1.52cm)^2)/((1.21cm)^2)\\\\n_l=1.58`