Question

A farmer plans to fence a rectangular corral. The diagonal distance from one corner of the corral to the opposite corner is five yards longer than the width of the corral. The length of the corral is three times the width. Find the length of the diagonal of the corral. Round your answer to the nearest tenth.

Answer 1

Length of diagonal is 7.3 yards.

Explanation:

Given: The diagonal distance from one corner of the corral to the opposite corner is five yards longer than the width of the corral. The length of the corral is three times the width.

To find: The length of the diagonal of the corral.

Solution: Let the width of the rectangular garden be x yards.

So, the length of the diagonal is
`x+5`

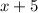
width of the rectangular corral is
`3x`

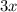
We know that the square of the diagonal is sum of the squares of the length and width.

So,

`(3x)^(2) +x^(2) =(x+5)^(2)`

`9x^(2) +x^(2) =x^(2)+10x+25`

`9x^(2)-10x-25=0`

`9x^(2)-10x-25=0`

`x=\frac{-b\pm\sqrt{b^(2) -4ac} }{2a}`

`x=\frac{10\pm\sqrt{(-10)^(2) -4(9)(-25)} }{2(9)}`

`x=(10\pm√(100))/(18)`

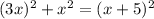
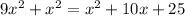
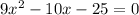
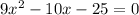
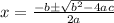
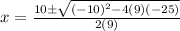
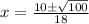
Since, side can't be negative.

`x=(5)/(9)+(5)/(9)√(10)`

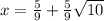
Now, length of the diagonal is

`5+(5)/(9)+(5)/(9)√(10)`

Hence, length of diagonal is 7.3 yards.