Question

In a sample of 388 people in a certain, 22% had red hair. Find a 99% confidence interval for the proportion of people in the country that have red hair.

Answer 1

Answer: (0.1658, 0.2742)

Explanation:

Formula to find the confidence interval for population proportion is given by :-

`\hat{p}\pm z^*\sqrrt{\frac{\hat{p}(1-\hat{p})}{n}}`

, where n= sample size

z*= Critical value

`\hat{p}` = sample proportion.

As per given , we have

Significance level :
`\alpha=1-0.99=0.01`

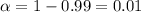
According to z-table, Critical value for 99% confidence interval : z*=2.576

Let p be the proportion of people in the country that have red hair.

n= 388

`\hat{p}=0.22`

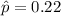
Now, required confidence interval for proportion of people in the country that have red hair will be :-

`0.22\pm (2.576)\sqrt{(0.22(1-0.22))/(388)}`

`0.22\pm (2.576)√(0.000442268)`

`0.22\pm (2.576)(0.02103)`

`(0.22-0.05417328,\ 0.22+0.05417328 )=(0.16582672,\ 0.27417328)\\\\\approx(0.1658,\ 0.2742)`

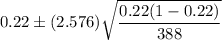
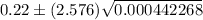
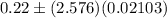
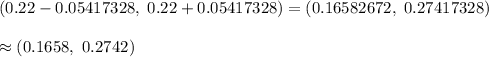
The 99% confidence interval for the proportion of people in the country that have red hair= (0.1658, 0.2742)