Question

. Helium is stored at 293 K and 500 kPa in a 1-cm-thick, 2-m-inner-diamater spherical container made of fused silica. The area where the container is located is well ventilated.

Determine

(a) the mass flow rate of helium by diffusion through the tank (15 points)

(b) the pressure drop in the tank after one week as a result of helium gas (10 points). Assume that the solubility of helium in fused silica is 0.00045 kmol/m3.bar.

Answer 1

(a) 45.17×10^-14 kg/s

(b) since the amount of helium escaped due to diffusion is insignificant, the final pressure drop in the tank remains the same as the initial pressure 500kPa.

Explanation:

Helium gas at temperature T=293k

Helium gas at pressure P= 500kPa

The inner diameter of spherical tank is
`D_1 = 2m`

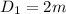
The inner radius of spherical tank is :
`r_1 = (D_1)/(2)`

=
`(2)/(2)`

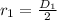
=1m

Thickness of the container r = 1cm =0.01m

Outer radius of the spherical tank is ;

t =
`r_2 - r_1`

`-r_2 = -t - r-1`

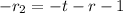
multiplying through with (-) we have ;

`r_2 = t + r_1`

`r_2 = 1 + 0.01m`

`r_2 = 1.01m`

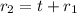
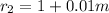
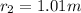
From table of binary diffusion coefficients of solids, the diffusion coefficients of helium in silica is noted as

`D_A_B =4.0 ×10^-14 (m^2)/(s)`

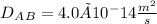
From table molar mass and gas constant, the molecular weight of helium is:

M = 4.003kg/kmol

The solubility of helium in fused silica is determined from Table of Solubility of selected gases and soilids.

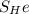`S_He` = 0.00045 kmol/m³. bar

Considering total molar concentration as constant, the molar concentration of helium inside the container is determined as

`C_B_I = S_H_e×P`

= 0.00045kmol/m³. bar × (5)

`C_B_I = 2.25×10^-3 kmol/m³`

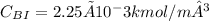
From one dimensional mass transfer through spherical layers is expressed as:

`N_di_f_f= 4πr_1 r_2 D_A_B (C_B_I - C_B_2)/(r_2 - r_1)`

substituting all the values in the above relation, we have;

`M_di_f_f= 4π(1) (1.01) (4.0×10^-14) (2.25 × 10^-3 -0)/(1.01-1)`

`M_di_f_f=11.42×10^-14kmol/s`

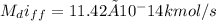
(a) The mass flow rate is expressed as

`M_di_f_f = MN_diff`

`M_di_f_f=4.003×11.42×10^-14`

`M_di_f_f=45.71×10^-14kg/s`

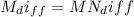
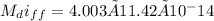
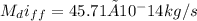
(b) The pressure drop in the tank after a week;

For one week the mass flow rate of helium is

`N_di_ff =11.42×10^-14kmol/s`

`N_di_ff= 11.42×10^-14×7×24×3600 kmol/week`

`N_di_f_f=6.9×10^-8kmol/week`

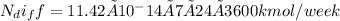
The volume of the spherical tank is
`V=(4)/(3) πr_1^3`

`V=(4)/(3)π×1^3`

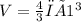
V = 4.189m³

The initial mass of helium in the sphere is determined from the ideal gas equation:

PV=NRT

where R is the universal gas constant and its value is R = 8.314 KJ/Kmol.k

N= PV/RT

N= 500 × 4.189/ 8.314 × 293

N= 0.86kmol

The number of moles of helium gas remaining in the tank after one week is:

`N_di_f_f-final = 0.86 - 6.9 × 10^-8 kmol/week`

`N_di_f_f-final ≅ 0.86`

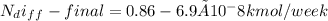
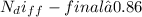
therefore, since the amount of helium escaped due to diffusion is insignificant, the final pressure drop in the tank remains the same as the initial pressure 500kPa.