Question

If the lens diameter is doubled, what happens to the resolvable angle of images produced at fixed wavelength?a. The angle decreases by a factor of two. b. The angle increases by a factor of four. c. The angle stays the same. d. The angle decreases by a factor of four.e. The angle increases by a factor of two.

Answer 1

Option A

Step-by-step explanation:

Angular resolution for any optical equipment can be defined as the ability of that tool to differentiate the smallest details of the image formed.

The angular resolution is given by:

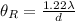`\theta_(R) = (1.22\lambda)/(d)` (1)

where

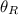`\theta_(R)` = Angular Resolution

`\lambda` = wavelength

d = diameter of the lens

Now,

As per the question:

If the diameter of the lens is doubled, i.e., d' = 2d

Then

From eqn (1):

`\theta'_(R) = (1.22\lambda)/(d') = (1.22\lambda)/(2d)`

`\theta'_(R) = (1)/(2)(1.22\lambda)/(d) = (1)/(2)\theta_(R)`

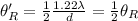
Thus when the diameter is doubled the angular resolution becomes half of its original value.