Answer:
1) 1829.3 and 1592.7 Hz, 2) 1963.8 and 1392.2 Hz, 3) 1948.9 Hz, 1404.5 Hz
Step-by-step explanation:
This is a doppler effect exercise, the police car is the sound source with a speed (
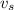 ) and the observer is stopped (v₀ = 0),
) and the observer is stopped (v₀ = 0),
In this configuration the equation that governs the doppler effect is
f’= (v + - v₀) / (v- +
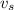 ) f
) f
Where v₀ is the observer's velocity, the positive sign is for when it approaches the source and
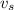 is the velocity of the source where the sign is for when it approaches the observer.
is the velocity of the source where the sign is for when it approaches the observer.
1) Let's calculate
The speed of sound in the air is v = 340 m / s
We reduce the speed of the car
vs = 120 km / h (1000m / 1 km) (1h / 3600s) = 33,333 m /s
Case 1. Police car approaching, still observer (v₀ = 0)
f’= (340 + 0) / (340 - 33.33) 1650
f’= 1.1087 1650
f’= 1829.3 Hz
Case 2. Police car moving away
f’= 340 / (340 + 33.33) 1650
f’= 0.9107 1650
f’= 1502.7 Hz
2) in this case both the source and the observed one move
Let's reduce the observer's car speed to SI units
v₀ = 90.0 km / h (1000m / 1 km) (1h / 3600s) = 25 m / s
Case 1. the cars approaching, we put the correct signs
f’= (340 + 25) / (340 - 33.33) 1650
f’= 1.19 1650
f’= 1963.8 Hz
Case 2 cars moving away
f’= (340 - 25) / (340 + 33.33) 1650
f’= 0.84376 1650
f’= 1392.2 Hz
3) in this case the two cars move, the observer's car (v₀)
v₀ = 80 km / h = 22.22 m / s
The cars initially approach as the police car goes faster, after a while the positive car passes to the other car and begins to move away
Case 1. Car approaching
f’= (340 + 22.22) / (340 - 33.33) 1650
f’= 1,181 1650
f’= 1948.9 Hz
Case 2. Cars moving away
f’= (340 - 22.22) / (340 + 33.33) 1650
f’= 0.8512 1650
f’= 1404.5 Hz