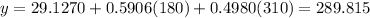Answer:
b) y = 289.815 when
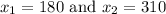
Explanation:
We are given the following information in the question:
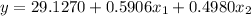
where y is the dependent variable,
 are the independent variable.
are the independent variable.
The multiple regression equation is of the form:
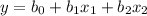
where,
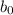 : is the intercept of the equation and is the value of dependent variable when all the independent variable are zero.
: is the intercept of the equation and is the value of dependent variable when all the independent variable are zero.
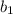 : It is the slope coefficient of the independent variable
: It is the slope coefficient of the independent variable
 .
.
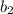 : It is the slope coefficient of the independent variable
: It is the slope coefficient of the independent variable
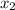 .
.
- The regression coefficient in multiple regression is the slope of the linear relationship between the dependent and the part of a predictor variable that is independent of all other predictor variables.
Comparing the equations, we get:
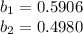
- This means holding
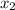 constant, a change of one in
constant, a change of one in
 is associated with a change of 0.5906 in the dependent variable.
is associated with a change of 0.5906 in the dependent variable.
- This means holding
 constant, a change of 1 in
constant, a change of 1 in
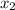 is associated with a change of 0.4980 in the dependent variable.
is associated with a change of 0.4980 in the dependent variable.
b) We have to estimate the value of y