Question

Use the diagonals to determine whether a parallelogram with the given vertices is a rectangle, rhombus, or square. Select the most specific name that applies. J(−8, −6), K(−3, −1), L(4, −2), and M(−1, −7)

Answer 1

The parallelogram is a rhombus.

Explanation:

Length of diagonal JL is =
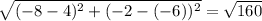`\sqrt{(- 8 - 4)^(2) + (- 2 - ( - 6))^(2) } = √(160)` units.

And the length of diagonal KM is =
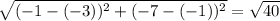`\sqrt{(- 1 - (- 3))^(2) + (- 7 - ( - 1))^(2) } = √(40)` units.

So, JL ≠ KM so, the parallelogram is neither rectangle nor a square.

Now, Slope of line JL =
`(-2 - ( - 6))/(4 - (- 8)) =  (1)/(3)`

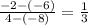
Again, slope of KM =
`(-7 - ( - 1))/(- 1 - ( - 3)) = - 3`

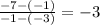
Therefore, the product of slope of JL and KM is - 1 and hence, JL ⊥ KM

And therefore, the parallelogram is a rhombus. (Answer)