Question

15A.4(a) What is the temperature of a two-level system of energy separation equivalent to 400 cm−1 when the population of the upper state is one-third that of the lower state?

Answer 1

T = 525K

Step-by-step explanation:

The temperature of the two-level system can be calculated using the equation of Boltzmann distribution:

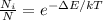`(N_(i))/(N) = e^(-\Delta E/kT)` (1)

where Ni: is the number of particles in the state i, N: is the total number of particles, ΔE: is the energy separation between the two levels, k: is the Boltzmann constant, and T: is the temperature of the system

The energy between the two levels (ΔE) is:

`\Delta E = hck`

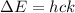
where h: is the Planck constant, c: is the speed of light and k: is the wavenumber

`\Delta E = 6.63\cdot 10^(-34) J.s \cdot 3\cdot 10^(8)m/s \cdot 4 \cdot 10^(4)m^(-1) = 7.96 \cdot 10^(-21)J`

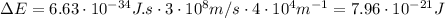
Solving the equation (1) for T:

`T = (-\Delta E)/(k \cdot Ln(N_(i)/N))`

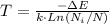
With Ni = N/3 and k = 1.38x10⁻²³ J/K, the temperature of the two-level system is:

`T = (-7.96 \cdot 10^(-21)J)/(1.38 \cdot 10^(-23) J/K \cdot Ln(N/3N)) = 525K`

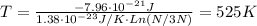
I hope it helps you!