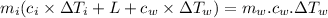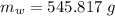Question

A 40.0-g block of ice at -15.00°C is dropped into a calorimeter (of negligible heat capacity) containing water at 15.00°C.

When equilibrium is reached, the final temperature is 8.00°C.

How much water did the calorimeter contain initially?

The specific heat of ice is 2090 J/kg • K, that of water is 4186 J/kg • K, and the latent heat of fusion of water is 33.5 × 104 J/kg.

Answer 1

`m_w=545.817\ g`

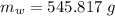
Step-by-step explanation:

Given:

• mass of ice block,
  `m_i=40\ g`

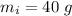
• initial temperature of ice block,
  `T_i_i=-15^(\circ)C`

• initial temperature of water,
  `T_i_w=15^(\circ)C`

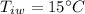
• final temperature of mixture,
  `T_f=8^(\circ)C`

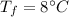
• specific heat of ice,
  `c_i=2.09\ J.g^(-1)`

• specific heat of water,
  `c_w=4.186\ J.g^(-1)`

• Latent heat of fusion of water,
  `L=335\ J.g^(-1)`

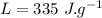
Now, assuming that there is no heat loss out of the mixture:

⇒ heat absorbed by the ice = heat rejected by the water

`m_i(c_i* \Delta T_i+L+c_w* \Delta T_w)=m_w.c_w.\Delta T_w`

`40(2.09* (0-(-15))+335+4.186* (8-0))=m_w* 4.186* (15-8)`

`m_w=545.817\ g`