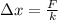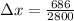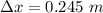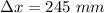Question

A 70.0-kg skier is sliding at 4 m/s when they slide down a 2m high hill. At the bottom of the hill they run into a large 2800 N/m spring.

How far do they compress the spring before coming momentarily to rest? Ignore friction.

Answer 1

`\Delta x=245\ mm`

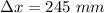
Step-by-step explanation:

Given:

• mass of skier,
  `m=70\ kg`

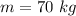
• initial velocity of skier,
  `u=4\ m.s^(-1)`

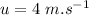
• height of the hill,
  `h=2\ m`

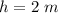
• spring constant,
  `k=2800\ N.m^(-1)`

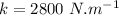
final velocity of skier before coming in contact of spring:

Using eq. of motion:

`v^2=u^2+gh`

`v^2=4^2+9.8* 2`

`v=5.9666\ m.s^(-1)`

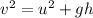
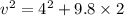
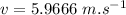
Now the time taken by the skier to reach down:

`v=u+gt`

`5.9666=4+9.8\ t`

`t=0.2007\ s`

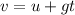
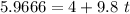
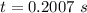
Now we calculate force using Newton's second law:

`F=(dp)/(dt)`

`F=(m(v-u))/(t)`

`F=(70*(5.9666-4))/(0.2007)`

`F\approx686\ N`

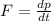
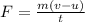
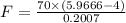
∴Compression in spring before the skier momentarily comes to rest:

`\Delta x=(F)/(k)`

`\Delta x=(686)/(2800)`

`\Delta x=0.245\ m`

`\Delta x=245\ mm`