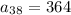Question

What’s the 38th term of the arithmetic sequence 31,40,49,58?

Answer 1

`a_3_8=364`

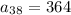
Explanation:

we know that

In an Arithmetic Sequence the difference between one term and the next is a constant, and this constant is called the common difference

we have

`31,40,49,58,...`

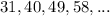
Let

`a_1=31\\a_2=40\\a_3=49\\a_4=58`

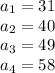
we have that

`a_2-a_1=40-31=9`

`a_3-a_2=49-40=9`

`a_4-a_3=58-49=9`

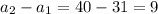
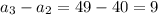
so

The common difference is equal to 9

We can write an Arithmetic Sequence as a rule:

`a_n=a_1+d(n-1)`

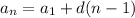
where

a_n is the nth term

a_1 is the first term

d is the common difference

n is the number of terms

Find the 38th term of the arithmetic sequence

we have

`a_1=31\\d=9\\n=38`

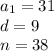
substitute the values

`a_3_8=31+9(38-1)`

`a_3_8=31+9(37)`

`a_3_8=364`