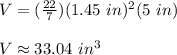1 Answer

Rherroral · Answer 1 · 2020-08-16T01:55:06+0000

Answer:
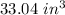
$33.04\ in^3$

Explanation:

The volume of a cylinder can be found with the following formula:

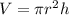
$V=\pi r^2h$

Where "r" is the radius and "h" is the height of the cylinder.

In this case, you know that the diameter of the can is:

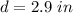
$d=2.9\ in$

Since the radius is half the diameter, this is:

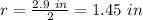
$r=(2.9\ in)/(2)=1.45\ in$

And the height is:

$h=5\ in$

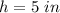
Therefore, substituting values into the formula and using
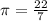$\pi =(22)/(7)$ , you get that the volume of the can, rounded to the nearest hundredth, is:

$V=((22)/(7))(1.45\ in)^2(5\ in)\\\\V\approx 33.04\ in^3$

Please log in or register to add a comment.