Question

Tarzan swings on a vine 30.0-m long initially inclined at an angle of 32.9 degrees to the vertical. If he pushes off with a speed of 3.30 m/s, what is his speed (in m/s) at the bottom of the swing if he starts from rest?

Answer 1

The velocity at the bottom of the swing is 9.71 m/s

Solution:

As per the question:

Length of the vine, l = 30.0 m

Incident angle,
`\theta = 32.9^(\circ)`

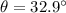
Speed, v = 3.30 m/s

Now,

From Fig. 1

AD = l

AB =
`lcos\theta`

AC =
`l - lcos\theta = l(1 - cos\theta)`

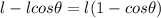
To calculate the speed at the bottom of the swing:

Initially at rest, i.e., initial velocity, v = 0 m/s

Potential Energy,
`PE = mgl - mglcos\theta = mgl(1 - cos\theta)`

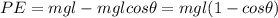
At the bottom of the swing:

Kinetic Energy,
`KE = (1)/(2)mv_(b)^(2)`

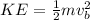
Now, by using the law of conservation of energy:

PE = KE

`mgl(1 - cos\theta) = (1)/(2)mv'^(2)`

`v_(b) = √(2gl(1 - cos\theta))`

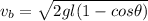
Substituting the appropriate value in the above eqn:

`v_(b) = √(2* 9.8* 30.0* (1 - cos32.9)) = 9.71\ m/s`