Answer:
The difference in the orbital periods of the satellites is zero.
Step-by-step explanation:
Given data,
The mass of the planet A is, m = 1.5 x 10² kg
The mass of the planet B is, m' = 4.5 x 10³ kg
The mass of the planet is, M = 6.6 x 10²⁴ kg
The orbital radius of the satellites are, R = 6.8 x 10⁶ m
The orbital period of the satellite is given by,
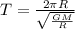
From the above equation, it is evident that the period of the satellite is independent of the mass of the satellite.
Since the radius of the orbit of the satellites A and B are the same, the difference in the orbital periods of the satellites is zero.