Answer:
The energy stored in capacitor B is four times the energy stored in capacitor A
Step-by-step explanation:
First let the write-out the formula for the energy stored in a capacitor in-terms of the capacitance(C)and the voltage(V)

For capacitor A charged to a voltage of V, The energy stored is

and for capacitor B, we have
![\\W_(B)=(1)/(2)C[2V]^(2)\\](https://img.qammunity.org/2020/formulas/physics/college/hy7h1kcax2pyrbff2i5ydse5m21xxiehi2.png)
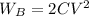
From the energy stored in Capacitor A we can arrive at
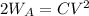
if we substitute this value into the energy for capacitor B we arrive at
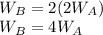
Hence we can conclude that the energy stored in capacitor B is four times the energy stored in capacitor A