Question

Jose left the science museum and traveled toward the capital at an average speed of 40mph. Wilbur left one hour later and traveled in the opposite direction with an average speed of 60 mph. How long does Wilbur need to travel before they are 540 miles apart?

Answer 1

The distance cover by Wilbur is 300 miles

Explanation:

Given as :

The average speed of the Jose =
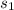`s_1` = 40 miles per hour

The Time taken by the Jose to travel =
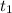`t_1` = T hours

The average speed of the Wilbur =
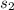`s_2` = 60 miles per hour

The Time taken by the Wilbur to travel =
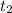`t_2` = ( T + 1 ) hours

The Distance cover by Jose =
`D_1` = D miles

The distance cover by Wilbur =
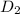`D_2` = (D - 540) miles

Now,

Distance = Speed × Time

Or,
`D_1` =
`s_1` ×
`t_1`

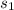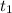
Or, D = 40 miles per hours × T hours ......1

∴ T =
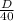`(D)/(40)` hours

Again

`D_2` =
`s_2` ×
`t_2`

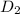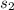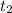
Or, 540 - D = 60 miles per hour × ( T - 1 ) hours

Or, D = 60 × ( T - 1 ) - 540 .....2

Solving Eq 1 and 2

I.e 40 × T = 60 × ( T + 1 ) - 540

or, 40 × T = 60 × T + 60 - 540

Or, 40 × T = 60 × T - 480

Or, 480 = 60 × T - 40 × T

Or, 480 = 20 T

∴ T =
`(480)/(20)` = 24 hours

So, From Eq 2

D = 60 × ( T - 1 ) - 540

Or, D = 60 × ( 24 - 1 ) - 540

Or, D = 60 × 23 - 540

∴ D = 840

So, The distance cover by Wilbur =
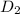`D_2` = (840 - 540) miles

I.e
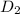`D_2` = 300 miles

Hence The distance cover by Wilbur is 300 miles . Answer