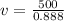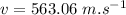Answer:
a)
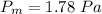
b)
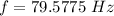
c)
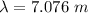
d)
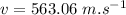
Step-by-step explanation:
Given equation of pressure variation:
![\Delta P= (1.78\ Pa)\ sin\ [(0.888\ m^(-1))x-(500\ s^(-1))t]](https://img.qammunity.org/2020/formulas/physics/high-school/yxfl1juxfaz3obyj08z30iqdw4tm3kny99.png)
We have the standard equation of periodic oscillations:
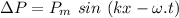
By comparing, we deduce:
(a)
amplitude:
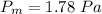
(b)
angular frequency:
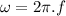
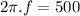
∴Frequency of oscillations:
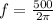
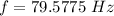
(c)
wavelength is given by:
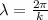
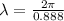
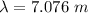
(d)
Speed of the wave is gives by: