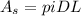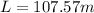Answer:

Step-by-step explanation:
Cold water in:

Hot water in:
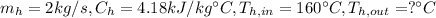

Step 1: Determine the rate of heat transfer in the heat exchanger
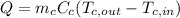


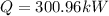
Step 2: Determine outlet temperature of hot water
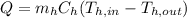
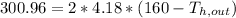
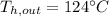
Step 3: Determine the Logarithmic Mean Temperature Difference (LMTD)

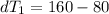

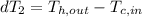
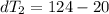
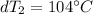
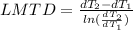
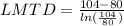
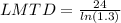
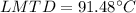
Step 4: Determine required surface area of heat exchanger


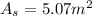
Step 5: Determine length of heat exchanger