Question

A garden hose with a diameter of 0.64 in has water flowing in it with a speed of 0.46 m/s and a pressure of 1.9 atmospheres. At the end of the hose is a nozzle with a diameter of 0.25 in.(a) Find the speed of water in the nozzle.(b) Find the pressure in the nozzle.

Answer 1

(a).The speed of the water in the nozzle is 3.014 m/s.

(b). The pressure in the nozzle is 1.86 atm.

Step-by-step explanation:

Given that,

Nozzle diameter = 0.25 in = 0.00635 m

Hose pipe diameter = 0.64 in = 0.016256 m

Pressure = 1.9 atm =192518 Pa

(a). We need to calculate the speed of the water in the nozzle

Flow Speed at the inlet pipe will be given by using Continuity Equation

`Q_(1)=Q_(2)`

`v_(1)A_(1)=v_(2)A_(2)`

`v_(1)=v_(2)*((A_(2))/(A_(1)))`

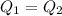
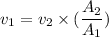
Where, A = area of pipe

`A=\pi* (d^2)/(4)`

`v_(1)=v_(2)*((d_(2)^2)/(d_(1)^2))`

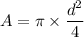
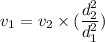
Put the value into the formula

`v_(1)=0.46*((0.016256)^2)/((0.00635)^2)`

`v_(1)=3.014\ m/s`

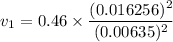
The speed of the water in the nozzle is 3.014 m/s.

(b). We need to calculate the pressure in the nozzle

Using Bernoulli's Theorem,

`P_(1)+(1)/(2)\rho* v_(1)^2+\rho gh_(1)=P_(2)+(1)/(2)\rho* v_(2)^2+\rho gh_(2)`

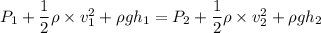
Where,
`h_(1)=h_(2)`

`P_(1)+(1)/(2)\rho* v_(1)^2=P_(2)+(1)/(2)\rho* v_(2)^2`

`P_(1)=P_(2)+(1)/(2)\rho(v_(2)^2-v_(1)^2)`

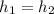
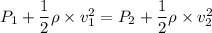
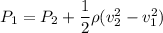
Put the value into the formula

`P_(1)=192518 +(1)/(2)*1000*((0.46)^2-(3.014)^2)`

`P_(1)=188081.702\ Pa`

`P=1.86\ atm`

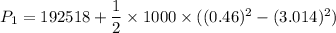
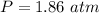
Hence, (a).The speed of the water in the nozzle is 3.014 m/s.

(b). The pressure in the nozzle is 1.86 atm.