Answer: 1.5 m/s
Step-by-step explanation:
In this problem we have to find the velocity of the second billiard ball after the collision.
According to the conservation of momentum law:
"If two objects or bodies are in a closed system and both collide, the total momentum of these two objects before the collision will be the same as the total momentum of these same two objects after the collision".
This means the initial momentum
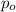 must be equal to the final momentum
must be equal to the final momentum
 :
:
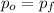 (1)
(1)
Where:
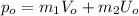 (2)
(2)
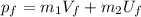 (3)
(3)
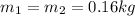 are the masses of each ball
are the masses of each ball
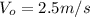 is the initial velocity of ball 1 (in the right direction)
is the initial velocity of ball 1 (in the right direction)
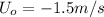 is the initial velocity of ball 2 (in the opposite direction)
is the initial velocity of ball 2 (in the opposite direction)
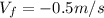 is the final velocity of ball 1 (in the opposite direction)
is the final velocity of ball 1 (in the opposite direction)
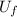 is the final velocity of ball 2
is the final velocity of ball 2
Substituting (2) and (3) in (1):
 (4)
(4)
Isolating
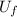 and remembering
and remembering
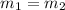 :
:
 (5)
(5)
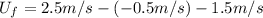 (6)
(6)
Finally:
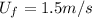 This is the final velocity of ball 2, directed to the right
This is the final velocity of ball 2, directed to the right