Question

A man stands on a platform that is rotating (without friction) with an angular speed of 2.4 rev/s; his arms are outstretched and he holds a brick in each hand. The rotational inertia of the system consisting of the man, bricks, and platform about the central vertical axis of the platform is 6.2 kg · m2. By moving the bricks the man decreases the rotational inertia of the system to 2.0 kg · m2. (a) What is the resulting angular speed of the platform? rev/s

Answer 1

The resulting angular speed of the platform is 7.44 rev/s.

Step-by-step explanation:

Given that,

Speed = 2.4 rev/s

Moment of inertia consist of the man = 6.2 kg-m²

Moment of inertia by the bricks= 2.0 kg-m²

We need to calculate the resulting angular speed of the platform

Using law of conservation of momentum

`L_(1)=L_(2)`

`I\omega_(1)=I\omega_(2)`

`\omega_(2)=(I_(1)\omega_(1))/(I_(2))`

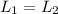
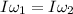
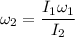
Where,

`I_(1)` = moment of inertia consist of the man

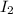`I_(2)` = moment of inertia by the bricks

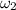`\omega_(2)` = angular speed of platform

Put the value into the formula

`\omega_(2)=(6.2*2.4*2\pi)/(2.0)`

`\omega_(2)=46.74\ rad/s`

`\omega_(2)=(46.74)/(2\pi)\ rev/s`

`\omega_(2)=7.44\ rev/s`

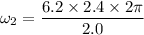
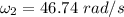
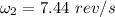
Hence, The resulting angular speed of the platform is 7.44 rev/s.