Question

A mass of 0.26 kg on the end of a spring oscillates with a period of 0.45 s and an amplitude of 0.15 m .a) Find the velocity when it passes the equilibrium point.b) Find the total energy of the system.c) Find the spring constant.d) Find the maximum acceleration of the mass.

Answer 1

a)V= 2.09 m/s

b)TE= 0.56 J

c)K=50.47 N/m

d)a=29.23 m/s²

Step-by-step explanation:

Given that

m = 0.26 kg , T= 0.45 s ,A= 0.15 m

We know that time period given as

`T=(2\pi)/(\omega)`

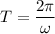
ω =Angular frequency

`{\omega}=(2\pi)/(T)`

`{\omega}=(2\pi)/(0.45)`

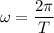
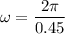
ω = 13.96 rad/s

The velocity at equilibrium

V= ω A

V= 13.96 x 0.15

V= 2.09 m/s

The total energy TE

`TE=(1)/(2)mV^2`

`TE=(1)/(2)* 0.26* 2.09^2`

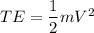
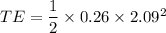
TE= 0.56 J

The spring constant K

Maximum stored energy in the spring

`U=(1)/(2)KA^2`

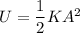
From energy balance

U= TE

`(1)/(2)KA^2=(1)/(2)mV^2`

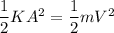
K A² = m V²

`=(mV^2)/(A^2)`

`K=(0.26* 2.09^2)/(0.15^2)`

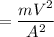
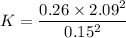
K=50.47 N/m

The maximum acceleration a

a= ω² A

a = 13.96² x 0.15 m/s²

a=29.23 m/s²