Question

A nickel crystal's work function is measured to be 5.22 eV at 25°C. As the temperature increases by 300°C, the work function drops by 50 meV.

By how much does this shift the threshold wavelength for photoelectric emission?

Answer 1

The shift the threshold wavelength for photoelectric emission is 2.317 nm.

Step-by-step explanation:

Given that,

Work function = 5.22 eV

Temperature = 25°C

Increased temperature = 300°C

Drop work function = 50 meV

We need to calculate the shift the threshold wavelength for photoelectric emission

Using formula of work function

`W=(hc)/(\lambda)`

`\lambda=(hc)/(W)`

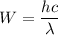
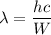
The wavelength for initial temperature,

`\lambda_(1)=(hc)/(W_(1))`

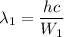
The wavelength for final temperature,

`\lambda_(2)=(hc)/(W_(2))`

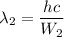
The change in wavelength is

`\Delta \lambd = \lambda_(2)-\lambda_(1)`

`\Delta \lambda=hc((1)/(W_(2))-(1)/(W_(1)))`

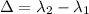
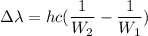
Put the value into the formula

`\Delta \lambda=2.001*10^(-25)((1)/(5.17*1.6*10^(-19))-(1)/(5.22*1.6*10^(-19)))`

`\Delta \lambda=2.317*10^(-9)\ m`

`\Delta\lambda=2.317\ nm`

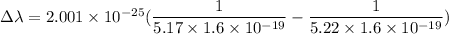
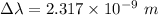
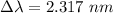
Hence, The shift the threshold wavelength for photoelectric emission is 2.317 nm.