Question

A system of equations is given below. y=1/2x-3 and -1/2x-3. Which of the following statements best describes the two lines?

They have the same slope but different y-intercepts, so they have no solution.
They have the same slope but different y-intercepts, so they have one solution.
They have different slopes but the same y-intercept, so they have no solution.
They have different slopes but the same y-intercept, so they have one solution.

Answer 1

The answer is D

Explanation:

Answer 2

"They have different slopes but the same y-intercept, so they have one solution" is the statement which best describes the two lines.

Answer: Option D

Explanation:

Given equations:

`y=\left((1)/(2) * x\right)-3`

`y=\left(-(1)/(2) * x\right)-3`

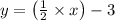
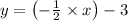
As we know that the slope intercept form of a line is

y = m x + c

So, from equation 1 and equation 2 we can see that

`m_(1)=(1)/(2) \quad \text { and } c_(1)=-3`

`m_(2)=-(1)/(2) \text { and } c_(2)=-3`

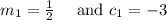
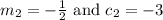
So, from the above expressions, we can say that both lines have different slopes but have same y – intercept with one common solution when x = 0.